이것 저것 공부하다가
흘러흘러가서 결국은 허프만 코드까지 공부하는 지경에 이르렀다.
전기과 출신(게다가 자퇴)에 디자이너 출신인 내 배경을 생각해보면
정말 장족의 발전이 아닐 수 없다. 허허...
아무튼 압축알고리즘의 가장 인기있는 알고리즘이 아닌가 한다.
MPEG 의 기본 압축 알고리즘으로도 쓰이고 있고
우리가 자주 사용하는 알집 역시 허프만 알고리즘으로 한번 압축한후
Lempel 이라는 간단한 압축알고리즘으로 한번 더 압축하는 프로세스라고 하니
허프만 알고리즘은 그 효율을 인정받고 있는듯 하다.
머 알고리즘이라고 해서
엄청 복잡한 줄 알았던 본인이지만
호프만 알고리즘을 보고 나서는
정말 무릎을 탁~ 치는 그런 느낌이었다.
다른 동영상 알고리즘이나 음향 알고리즘은
무슨 주파수에 양자화니 빈도수 머 어쩌구 저쩌구...
먼말인지 하나도 모르겠지만
호프만 알고리즘의 핵심은 두가지로 설명할 수 있다.
1. 이론
자주 쓰이는 문자에 가장 작은 bit 를 할당하고
한두번 쓰이는 문자에는 큰 bit 를 할당한다라는 것이다.
즉 간단하게 예를 들어서
AABBAC
라는 문자열이 있다고 예를 들어보자.
영문자 하나는 1byte 이므로 총 6byte 의 크기를 가지는 문자열이다.
자 그럼
각 문자들이 사용된 횟수를 알아보자.
머 짧으니까 한눈에 알 수 있을 것이다.
A 는 3번
B 는 2번
C 는 1번 사용되었다.
그러면 가장 많이 사용된 A 에게 0 이라는 1bit 를 부여하고
B 는 10, C 는 11 을 부여할 수 있다.
그러면 위 문자열은
A(0)A(0)B(10)B(10)A(0)C(11)
합쳐보면 001010011 로 나타낼 수 있다.
총 9 bit = 1 byte + 1 bit 으로 압축을 할 수 있다.
원래 문자열이 6 byte 즉 48 bit 를 차지하였는데 9/48 = 0.19
즉 약 20% 로 압축이 되었다. 압축률이 80% 라는 이야기다.
뭐 조금 띄엄띄엄 살펴본것 같지만 허프만 알고리즘의 핵심은 바로 이것이다.
물론 헤더도 붙고 하다보면 조금더 커지겠지만
큰 파일일 수록, 텍스트 기반일 수록, 자주 쓰이는 문자가 많을 수록 압축률은 높아지게 되어 있다.
2. 이진 트리
자 그렇다면 이론은 알겠는데
실제로는 어떻게 적용해야하는 걸까?
순서대로 한번 살펴보자.
대상 문자열 : CDDCACBCBCCCBBCDA
1. 각 문자열별로 빈도수를 검사한다.
2. 빈도수 순서대로 정렬한다. (repeat 1/2)
3. 가장 낮은 두 그룹을 묶어서 하나의 그룹으로 만든다. (repeat 2/2)
4. 빈도수 순서대로 정렬한다. (repeat 1/2)
5. 가장 낮은 두 그룹을 묶어서 하나의 그룹으로 만든다. (repeat 2/2)
6. 빈도수 순서대로 정렬한다. (repeat 1/2)
7. 가장 낮은 두 그룹을 묶어서 하나의 그룹으로 만든다. (repeat 2/2) 트리완성.
8. 이제 트리가 완성되었다.
가장 윗 트리에서부터 빈도수가 큰 트리에 0을 작은 트리에 1을 부여한다.
9. 위 트리를 기준으로 각 문자열의 비트를 참조한다.
부모노드에서 출발하여 문자열에 다다를때까지 비트를 더하여 참조한다. 즉,
A - 001 이 된다.
이와 같은 방법으로
B - 01, C - 1, D - 000 로 비트를 할당 할 수 있게 된다.
그러면 초기 문자열을 할당된 비트로 치환하여 보자.
1000000100110110111101011000001
위와 같이 치환되었다.
총 17문자, 17 byte 였던 원래 문자열이 31 bit 즉, 8 byte 로 압축이 된것이다.
물론 문자열 테이블도 붙고 헤더도 붙으면 약간 더 늘어나겠지만
이번 테스트에서의 압축률은 약 50%로 나타났다.
3. 디코딩은?
호프만 알고리즘을 이용하여 압축을 하면
어떤 문자가 어떤 bit 로 치환되었는지를 판단해야되기 때문에
호프만 테이블이라고 불리는 테이블을 추가해야한다.
호프만 테이블은 방금 우리가 만든 그 이진 트리를 말한다.
그 트리를 보고 복호화하는것이다.
한 bit 단위로 읽어서 테이블대로
문자가 나올때까지 트리를 타고 가면서 치환하는것이다.
예를 들어 00101 이라는 데이타는
AB 를 나타낸다는 것이다.
- 00101 을 복호화해보자
- 첫 비트 0 은 17로 표시되어 있는 트리에서 왼쪽, 즉 9 로 표시되어 있는 트리로 내려간다.
- 다음 0 은 역시 왼쪽, 5 로 표시되어 있는 트리로 내려간다.
- 다음 1 비트는 오른쪽, 즉 2로 표시되어 있는 트리, A 를 나타낸다.
- 문자를 하나 찾았으니 자 그럼 다시 처음부터
- 다음 0 은 17 트리에서 9 트리로
- 다음 1 은 오른쪽 4 트리로, 즉 B 를 나타낸다.
이런식으로 문자열을 치환해주면된다.
대단하지 않은가??
이게 바로 허프만 알고리즘의 원리인것이다.
흘러흘러가서 결국은 허프만 코드까지 공부하는 지경에 이르렀다.
전기과 출신(게다가 자퇴)에 디자이너 출신인 내 배경을 생각해보면
정말 장족의 발전이 아닐 수 없다. 허허...
아무튼 압축알고리즘의 가장 인기있는 알고리즘이 아닌가 한다.
MPEG 의 기본 압축 알고리즘으로도 쓰이고 있고
우리가 자주 사용하는 알집 역시 허프만 알고리즘으로 한번 압축한후
Lempel 이라는 간단한 압축알고리즘으로 한번 더 압축하는 프로세스라고 하니
허프만 알고리즘은 그 효율을 인정받고 있는듯 하다.
머 알고리즘이라고 해서
엄청 복잡한 줄 알았던 본인이지만
호프만 알고리즘을 보고 나서는
정말 무릎을 탁~ 치는 그런 느낌이었다.
다른 동영상 알고리즘이나 음향 알고리즘은
무슨 주파수에 양자화니 빈도수 머 어쩌구 저쩌구...
먼말인지 하나도 모르겠지만
호프만 알고리즘의 핵심은 두가지로 설명할 수 있다.
1. 이론
자주 쓰이는 문자에 가장 작은 bit 를 할당하고
한두번 쓰이는 문자에는 큰 bit 를 할당한다라는 것이다.
즉 간단하게 예를 들어서
AABBAC
라는 문자열이 있다고 예를 들어보자.
영문자 하나는 1byte 이므로 총 6byte 의 크기를 가지는 문자열이다.
자 그럼
각 문자들이 사용된 횟수를 알아보자.
머 짧으니까 한눈에 알 수 있을 것이다.
A 는 3번
B 는 2번
C 는 1번 사용되었다.
그러면 가장 많이 사용된 A 에게 0 이라는 1bit 를 부여하고
B 는 10, C 는 11 을 부여할 수 있다.
그러면 위 문자열은
A(0)A(0)B(10)B(10)A(0)C(11)
합쳐보면 001010011 로 나타낼 수 있다.
총 9 bit = 1 byte + 1 bit 으로 압축을 할 수 있다.
원래 문자열이 6 byte 즉 48 bit 를 차지하였는데 9/48 = 0.19
즉 약 20% 로 압축이 되었다. 압축률이 80% 라는 이야기다.
뭐 조금 띄엄띄엄 살펴본것 같지만 허프만 알고리즘의 핵심은 바로 이것이다.
물론 헤더도 붙고 하다보면 조금더 커지겠지만
큰 파일일 수록, 텍스트 기반일 수록, 자주 쓰이는 문자가 많을 수록 압축률은 높아지게 되어 있다.
2. 이진 트리
자 그렇다면 이론은 알겠는데
실제로는 어떻게 적용해야하는 걸까?
순서대로 한번 살펴보자.
대상 문자열 : CDDCACBCBCCCBBCDA
1. 각 문자열별로 빈도수를 검사한다.

2. 빈도수 순서대로 정렬한다. (repeat 1/2)

3. 가장 낮은 두 그룹을 묶어서 하나의 그룹으로 만든다. (repeat 2/2)
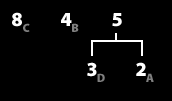
4. 빈도수 순서대로 정렬한다. (repeat 1/2)
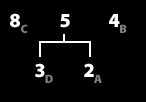
5. 가장 낮은 두 그룹을 묶어서 하나의 그룹으로 만든다. (repeat 2/2)
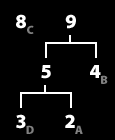
6. 빈도수 순서대로 정렬한다. (repeat 1/2)
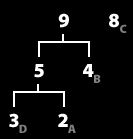
7. 가장 낮은 두 그룹을 묶어서 하나의 그룹으로 만든다. (repeat 2/2) 트리완성.
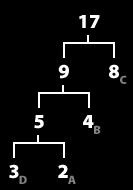
8. 이제 트리가 완성되었다.
가장 윗 트리에서부터 빈도수가 큰 트리에 0을 작은 트리에 1을 부여한다.
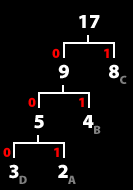
9. 위 트리를 기준으로 각 문자열의 비트를 참조한다.
부모노드에서 출발하여 문자열에 다다를때까지 비트를 더하여 참조한다. 즉,
A - 001 이 된다.
이와 같은 방법으로
B - 01, C - 1, D - 000 로 비트를 할당 할 수 있게 된다.
그러면 초기 문자열을 할당된 비트로 치환하여 보자.
1000000100110110111101011000001
위와 같이 치환되었다.
총 17문자, 17 byte 였던 원래 문자열이 31 bit 즉, 8 byte 로 압축이 된것이다.
물론 문자열 테이블도 붙고 헤더도 붙으면 약간 더 늘어나겠지만
이번 테스트에서의 압축률은 약 50%로 나타났다.
3. 디코딩은?
호프만 알고리즘을 이용하여 압축을 하면
어떤 문자가 어떤 bit 로 치환되었는지를 판단해야되기 때문에
호프만 테이블이라고 불리는 테이블을 추가해야한다.
호프만 테이블은 방금 우리가 만든 그 이진 트리를 말한다.
그 트리를 보고 복호화하는것이다.

한 bit 단위로 읽어서 테이블대로
문자가 나올때까지 트리를 타고 가면서 치환하는것이다.
예를 들어 00101 이라는 데이타는
AB 를 나타낸다는 것이다.
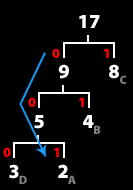
- 00101 을 복호화해보자
- 첫 비트 0 은 17로 표시되어 있는 트리에서 왼쪽, 즉 9 로 표시되어 있는 트리로 내려간다.
- 다음 0 은 역시 왼쪽, 5 로 표시되어 있는 트리로 내려간다.
- 다음 1 비트는 오른쪽, 즉 2로 표시되어 있는 트리, A 를 나타낸다.
- 문자를 하나 찾았으니 자 그럼 다시 처음부터
- 다음 0 은 17 트리에서 9 트리로
- 다음 1 은 오른쪽 4 트리로, 즉 B 를 나타낸다.
이런식으로 문자열을 치환해주면된다.
대단하지 않은가??
이게 바로 허프만 알고리즘의 원리인것이다.
'Adobe AIR > AIR 강좌' 카테고리의 다른 글
| [AIR] 완성도 높은 어플리케이션을 만들어 보자. (7) | 2008.07.25 |
|---|---|
| [AIR] AIR runtime 자동 업데이트 비활성화 (2) | 2008.03.17 |
| [AIR 강좌] XML 파일 만들고 저장하기 2부. (6) | 2007.10.31 |
| [AIR 강좌] XML 파일 만들고 저장하기 1부. (0) | 2007.10.31 |
| [AIR] NativeWindow 띄우기 (4) | 2007.08.28 |